Problem
Starting in the top left corner of a 2*2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
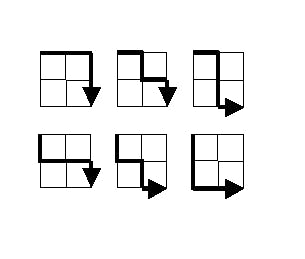
How many such routes are there through a 20*20 grid?
Problem Description
We are given a 2*2 grid and the number of paths to travel from the top-right corner to the bottom-left corner are 6 routes. Note that it is from the top-right corner to the bottom-right corner and not from the top-right cell to the bottom-right cell.
In a n*m grid, we have (n + 1) * (m + 1) corners or points through which we trace the path.
At any given point, we can either move RIGHT or DOWN. No other direction is possible.
Now, we must find the number of such paths in a 20*20 grid.
Approach
Well, this is another problem that gave me sleepless nights. I had to do some research before figuring out the best solution. 🧾
First let's understand what is a Lattice, and a Lattice Path. 🤔
Lattice Points & Lattice Paths:
A Lattice point is a repeating point arranged in a pattern like a square, rectangle or hexagon. The below diagram is a 2D square lattice arrangement.

Now, the lattice path is a sequence of steps connecting adjacent lattice points. Also, we restrict the movement to two directions, one-way horizontal and one-way vertical.
Since we are starting from the top-left corner, we move either RIGHT or DOWN.

Counting the Paths:
In the given problem, all possible lattice paths in a 2*2 grid is calculated as 6 paths. Remember, we can either go Right or Down.
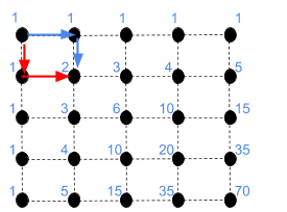
One way to count lattice paths is by adding the number of ways in which we can reach each dot in the lattice. Remember, we can only go RIGHT or DOWN and always start from the same corner.
In the example 4x4 lattice below, the blue and red paths indicate two possible ways to get to the first bottom-right point. So, we marked it with a 2.
In the same way, to reach the next point, we calculate that there are 3 possible paths(2 from left & 1 from top), marked in blue, green and red.
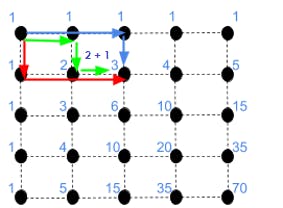
And for the next point to the right, there are 4 possible paths (3 from left & 1 from top) and so on.
All the points along the left are marked with 1. From the top-left corner to the bottom-left corner, there is only one path available - remember we can either move RIGHT or DOWN. In the same way, all the points along the top are marked with 1.
Following this process, we count all paths till the desired point.
We use a few methods to count the lattice paths and can be used to count the paths of a lattice of any size. Let us consider the above 4 * 4 grid and assign cartesian coordinates to each dot in the lattice for path calculation.
The top-left corner is marked as (0, 0) and the bottom-right corner is marked as (4 4). Let us count the paths from (0, 0) to (3, 4) in this grid (marked in red).

Method 1: Recursive method
In this method, we count the paths recursively from (3, 4) to (0, 0). That is, from (m, n) to (0, 0). Using variables, (m, n) is (3, 4).
On one look at the diagram above, we can say that the number of paths from (0, 0) to (3, 4) is equal to the number of paths from (0, 0) to (2, 4) plus the number of paths from (0, 0) to (3, 3).
Thus, to count the path at (m, n) we use (0, 0) -> (m-1, n) + (0, 0) -> (m, n-1).
This way, we calculate the path recursively till (0, 0) and add all the counts. When it is at any of the 0 coordinates, we return 1.
function countPath(m, n)
if n = 0 or m = 0 then
return 1
else
return countPath(m-1, n) + countPath(m, n-1)
end function
But this is too slow to answer in a reasonable time. If time constraints or space constraints are involved, then it would eventually time out. If you are executing this solution in Hackerrank, then it would time out for more than half of your test cases.
Method 2: Dynamic Programming or Iterative method
Instead of starting from m = 20 & n = 20 and counting all the way to m = 0 & n = 0, we start from our base all the way to the desired point, saving our result in a 2D-like array.
This approach is more like dynamic programming, where we use grid[i][j] for every point. I have not tried this method yet.
Method 3: Combinatorics
The number of lattice paths from (0, 0) to (m, n) is equal to the number of combinations of m objects out of m + n options. And the formula for counting the number of combinations m out of n objects(n choose m) is,
$${k}C_n = \frac{k!}{(k - n)! * n!} where (k = m + n)$$
At the location (3, 4), m = 3 and n = 4. Then the number of lattice paths is the combination of m = 3 out of m + n = (3+4) = 7 options.
In other words, it's the number given by "7 choose 3", which is,
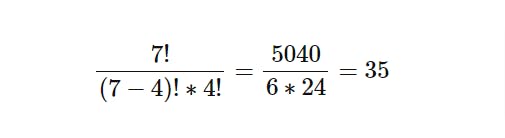
And that is the number of lattice paths from (0, 0) to (3, 4) in the above 4 * 4 grid.
Similarly, we can calculate for 20 * 20 grid.
Method 4: Binomial Coefficient
The count at the point (n, m) corresponds to the binomial coefficient,
$$\binom{n + m}{m} OR \binom{n + m}{n}$$
which is equivalent to the "n + m choose m" or "n + m choose n" expression from the above combinatorics. The formula used is the same as above where k = n + m
$$\binom{k}{n} = \frac{k!}{(n - k)! * n!}$$
Method 5: Pascal's Triangle
There is another method where the binomial coefficient is arranged in pascal's triangle from which we can count the number of lattice paths in the n * m grid. No, I have not tried this method too. You can refer to the wiki link provided at the end of this post for more information.
Note: Please note that the solution provided is only for learning purposes. Once you understand the problem, please try it on your own before referring to my solution below.
Solution
const latticePathsRecursive = (m, n = m) => {
if (m < 0 || n < 0) return 0; // to make sure of any negatives
if (m === 0 && n === 0) return 1;
return (latticePathsRecursive(m - 1, n) + latticePathsRecursive(m, n - 1));
}
const latticePathsCombinatorics = (m, n) => {
const factorial = (number) => {
if (number === 1 || number === 0) {
return 1;
} else {
return number * factorial(number - 1);
}
}
let k = m + n;
let res = factorial(k) / (factorial(k-n) * factorial(n));
return res;
}
console.log(latticePathsCombinatorics(4, 4)); // 70
console.log(latticePathsCombinatorics(3, 4)); // 35
console.log(latticePathsCombinatorics(20, 20)); // 137846528820
You can find my solution on GitHub 15
For Hackerrank, the recursive method timed out for 8 out of 11 test cases. But the combinatorics method worked fine along with BigInt and the modulo (1000000007) given in the problem.
If you have any feedback, please leave it below.
If you have any suggestions to improve my code or another way to approach this problem, leave it in the comment.
For the other project Euler solutions, please follow the series Project Euler Solutions in JS.
Thank you!
Reference note:
Most of the diagrams here are from stemhash.com. My examples are based on these diagrams.
Refer to these wiki pages for more on Lattice and binomial coefficients.
Another great video source on Binomial Coefficients & Lattice paths is here.
One of the best stackoverflow answers that explain the concept.
